Baudhayana - The Man who knew Pythagoras-Theorem 1000 years before Birth of Pythagoras

Budhayana

Sanskrit (संस्कृत):बौधायन

Birth:800 BC(approx.)

Decreased: 740 BC

Country: present-day Bharat(India)

He was a Mathematician, a priest and an architect of very high standards. It is possible that Baudhayana’s interest in Mathematical calculations stemmed more from his work in religious matters than a keenness for mathematics as a subject itself. Undoubtedly he wrote the Sulbasutra शुल्बसूत्र to provide rules for religious rites, and it would appear almost certain that Baudhayana himself would be a Vedic priest.Sulbasutra शुल्बसूत्र provide techniques to solve mathematical problems effortlessly.

If a ritual was to be successful, then the altar had to conform to very precise measurements. Therefore mathematical calculations needed to be precise with no room for error.
People made sacrifices to their gods for the fulfilment of their wishes. As these rituals were meant to please the Gods, it was imperative that everything had to be done with precision. It would not be incorrect to say that Baudhayana’s work on Mathematics was to ensure there would be no miscalculations in the religious rituals. There is a lot of emphasis on rectangles and squares in Baudhayana’s works.

Baudhayana theorem

Baudhāyana listed Pythagoras theorem in his book called Baudhāyana Śulbasûtra बौधायन शुलबसूत्र:

दीर्घचतुरश्रस्याक्ष्णया रज्जु: पार्श्र्वमानी तिर्यग् मानी च यत् पृथग् भूते कुरूतस्तदुभयं करोति ॥

Here he has used example of a rope for explanation as follows; 

The areas produced separately by the length and the breadth of a rectangle together equal the areas produced by the diagonal.

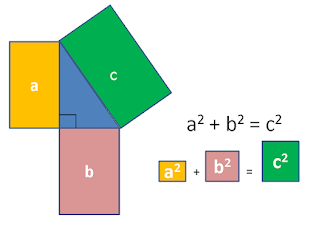
c is the longest side of the triangle(this is called the hypotenuse) with a and b being the other two sides
 Baudhayana used area calculations and not geometry to prove his calculations.

Method of finding √2

He gives the length of the diagonal of a square in terms of its sides, which is equivalent to a formula for the square root of 2. The measure is to be increased by a third and by a fourth decreased by the 34th. 

समस्य द्विकर्णि प्रमाणं तृतीयेन वर्धयेत।

तच् चतुर्थेनात्मचतुस्त्रिंशोनेन सविशेषः। ।

समस्य  Square  

 द्विकर्णि     Diagonal (dividing the square into two), or Root of Two

प्रमाणं     Unit measure

तृतीयेन वर्धयेत  increased by a third

तच् चतुर्थेन that itself increased by a fourth

आत्म  itself

चतुस्त्रिंशोनेन  सविशेषः  is in excess by 34^th part

which means accurate to 5 decimal places

Value of π  

He was first to discover the value of π

According to his premise, the approximate value of pi is $3$.

Several values of π occur in Baudhayana's Sulbasutra, since, when giving different constructions, Baudhayana used different approximations for constructing circular shapes.

Some of these values are very close to what is considered to be the value of pi today, which would not have impacted the construction of the altars. Although, his value was not accurate as that of Aryabhata.

Area of circle (approx.) equal in area to a square and vice versa

These procedures are described in his sutras (I-58 and I-59)

possibly in his quest to construct circular altars, he constructed two circles circumscribing the two squares shown below.

 Now, just as the areas of the squares, he realised that the inner circle should be exactly half of the bigger circle in area. He knew that the area of the circle is proportional to the square of its radius and the above construction proves the same. By the same logic, just as the perimeters of the two squares, the perimeter of the outer circle should also be $\sqrt{2}$ times the perimeter of the inner circle. This proves the known fact that the perimeter of the circle is proportional to its radius. This led to an important observation by Baudhayana. That the areas and perimeters of many regular polygons, including the squares above, could be related to each other just as the case of circles.

His Some Treatises

In any rhombus, the diagonals (lines linking opposite corners) bisect each other at right angles (90 degrees)

The diagonals of a rectangle are equal and bisect each other.

The midpoints of a rectangle joined forms a rhombus whose area is half the rectangle.

The area of a square formed by joining the middle points of a square is half of the original one.